直線と直線の交点を計算してみようと思います。
2つの直線、「ax+by+c=0」と「gx+hy+i=0」があるとき、それらが交わるかどうかは、平行であるかどうかを調べればわかります。これは外積で判別できます。
ベクトルv1[x,y]とベクトルv2[x,y]の外積 v1.x*v2.y - v1.y*v2.x = v1.length*v2.length*Math.sin(radian)
この場合、ベクトル(a,b)とベクトル(g,h)の外積が0の場合、sinが0になるので平行ということになります。
で、交点の位置は、下図のようにベクトルv1、ベクトルv2をおいたとき、ベクトルwは、w=k1*v1+k2*v2 で表現できます。k1,k2は係数で、この係数を求めます。
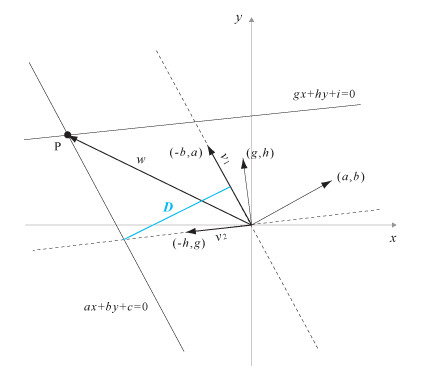
このとき、Dに注目すると、これは直線「ax+by+c=0」と原点の距離で、-c/v1.length です。一方、v1とv2のなす角度から考えると、v2.length*Math.sin(θ)のk2倍とDは等しくなります。
D = -c/v1.length = k2 * v2.length*Math.sin(θ) ↓ k2 = -c/( v1.length*v2.length*Math.sin(θ) ) ←ここが外積になる ↓ k2 = -c/(-b*g + h*a)
同様に、k2を求めると、
k1 = i/(-b*g + h*a)
になります。
w=k1*v1+k2*v2 なので、
w = ( k1*-b + k2*-h , k1*a + k2*g ) cross = -b*g + h*a ↓ w = ( ( -i*b + c*h)/cross , (i*a - c*g)/cross )
スクリプトにすると、
var cross:Number = -b*g + h*a;
if( cross!=0 ){
//交点
return new Point( (-b*i + c*h)/cross , (i*a - c*g)/cross );
}else{
//2つの直線は平行
return null;
}
になります。