| INDEX |

[as]直線と点の距離

10月 5, 2007

直線と点の距離をActionScriptで計算してみようと思います。非常に月並みですが、地味な感じですが。


直線は、例えば「y=ax+b」で表現されますが、一般的には「ax+by+c=0」になります。
この式の意味するところは、c=0 のとき、「ax+by=0」を考えるとわかりやすいかもしれません。

係数a,bをベクトルv、座標(x,y)をベクトルw1とすると、「ax+by=0」というのは、vとw1の内積になります。 

ベクトルv1[x,y]とベクトルv2[x,y]の内積
v1.x*v2.x + v1.y*v2.y = v1.length*v2.length*Math.cos(radian)

内積が常に0になる、ということなので、Math.cos(radian)が常に0になるということです。
つまり、w1は常にvに対して垂直なベクトルになります。この点の集合が直線になります。

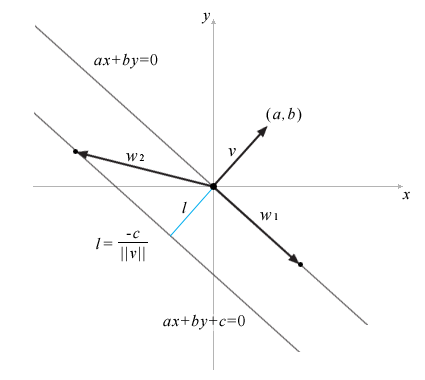
次に、直線「ax+by+c=0」ですが、先ほどと同じく、内積が常に-cになるベクトルw2の点の集合になります。
ここで、直線と原点の距離ｌは、 

v.length*w2.length*Math.cos(radian) = -c
　↓
Math.cos(radian) = -c/(v.length*w2.length)
Math.cos(radian) = l/w2.length
　↓
l = -c/v.length

になります。
で、ここから直線「ax+by+c=0」と点「p」の距離です。

点「p」を通り「ax+by+c=0」と平行な直線を「ax+by+d=0」とします。この２つの直線の距離は、直線と点の距離に同じです。
それぞれの原点からの距離の差になるので、 

距離 = (-d/v.length) - (-c/v.length)

dは、d=-a*x-b*y → d=-a*p.x-b*p.y なので、 

距離 = ( a*p.x + b*p.y + c)/v.length

になります。距離が得られれば、点から直線へ下ろした垂線のベクトルを得ることもできます。関数にするとこんな感じ。 

// 直線:ax+by+c=0
/**
* 直線と点の距離
* @param	Point
* @return	距離
*/
public function distanceToPoint( p:Point ):Number{
  return Math.abs( a*p.x + b*p.y + c )/Math.sqrt( a*a + b*b );
}

/**
* 点から直線へのベクトル
* @param	Point
* @return	Vector
*/
public function vectorFromPoint( p:Point ):Point{
  //距離
  var v:Point = new Point( a, b );
  v.normalize( -( a*p.x + b*p.y + c )/v.length );
  return v;
}

なにか長々してしまいました。

| INDEX |