最近は季節変動で呼吸器系をやられつつゲームやり過ぎな毎日ですが、2つの2次ベジェ曲線の交点について簡単に書いてみます。最初は幾何学的に解けるんじゃないかと考えていたのですが、結局は数値解析的な方法で求めました。Bezier Clipping 法の考え方(FatLine)を参考にしています。

交点を求める過程の基本的な考え方は次のような感じです。

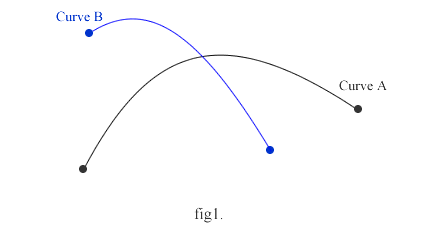
図のように曲線Aと曲線Bがあるとき、一方の曲線を包括する矩形を求めます。この矩形は、曲線の始点、終点を水平にしたときのgetRectに相当します。この矩形で、fig2のように一方の曲線を切り出します。

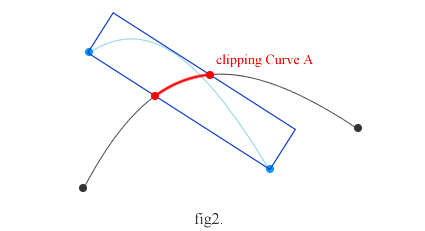
上図の場合、一本の曲線が切り出されていますが、場合によっては複数本の曲線が切り出されることになります。

次に、切り出した曲線について同じように矩形を求めて、他方の曲線を切り出すわけです。

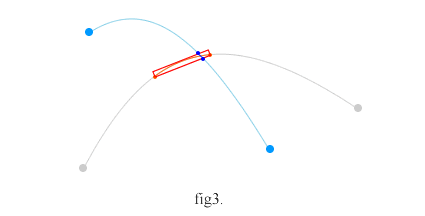
この、曲線の矩形化・曲線切り出しの処理を繰り返すと、最終的に矩形が直線と見なせるぐらいのサイズになり、交点の近似値を得ることができます。近似で求められるのは座標値になります。例によって使いどころが殆どなさそうな処理ですが…。

ちなみに、交点の近似座標からベジェ関数の値(0～1)を求める場合は、曲線と点の最近傍の値を計算して得ることもできます。

//var bezier:QBezier;
//var intersection_point:Point;
var t:Number = QBezierUtil.nearestFromPoint( bezier, intersection_point );

>> source
※ソース中のパッケージは、[3次ベジェ2次ベジェ変換]のときと同じです。