正直忘れてしまいそうなのでエントリしてみようと思いました。説明はぐだぐだやもですが…。で、3次ベジェから2次ベジェの近似変換について簡単に書いてみます。ソースには2次から3次も書いてありますが、使うことあるのかなぁ的でメモ的に書いているだけです。
今回実装している3次から2次の変換は、まず3次ベジェが一つの2次ベジェで表現できるかチェック、その後段階的に2次ベジェの数を増やして複数の曲線で近似する流れになっています。
一つの2次で表現できるかは下図のような考えで行います。
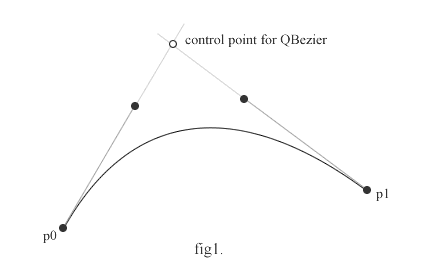
3次ベジェのコントロール点の延長にある交点を、2次ベジェのコントロール点にしてみるわけです。大抵の場合一致はしません…。
次に複数の曲線の組み合わせを試してみます。基本的な方法は3次ベジェを二つの2次ベジェで表現してみることです。
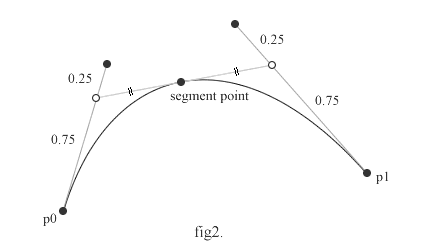
この方法を基本として、最初に3次ベジェを二つの2次ベジェ、次に3次ベジェを分割し、それぞれの3次ベジェを二つの2次ベジェに(合計4曲線)する。以降、3次ベジェを適当に分割しながら、その倍数の2次ベジェで表現してみるわけです。今回のものは、2次ベジェの数でいうところの、2、4、6、8で近似しています。大抵の場合、8つの2次ベジェで近似できます。
で、各段階で近似OKかどうかを、何点かのサンプル点での曲線の傾きと曲線の長さで判断しています。傾きは曲線を微分して求めます。長さだけでも大体近似できるわけですが、捻れた曲線などの場合にずれることがあるので傾きチェックを入れているわけです。
しかしまぁ、使いどころはかなり限られていますね。ちなみに、3次ベジェを変換してcurveToで描画するのと、3次ベジェ関数を計算しながら点を結んで描画していくのでは後者の方が速いです。曲線を動かしながら描画するなら変換はせんほうがええということですね。んか、もっと効率のよい方法があるとおもいました。
なにげにMITライセンスを書いてみたりした、というより書いてみたかった興味…。ホルダーの記述があやしい…よくわかりません。