| INDEX |

x = x + (d – x) / 2.0 のこと

8月 11, 2009

yossyさんが「x = x + (d – x) / 2.0 を時間に基づく関数に変換する」というエントリをアップしていたので、少し違う方面から解いてみる。結論から言えば結果は同じなんですが…、こういった問題はわりと見た目？から考える性格なのでちょっとやってみます。というかこういうこと考えるの好きで…。

とりあえず問題の式です。dは目標値、kは比率(0<k<1)です。 

x' = x + ( d - x ) * k (式1)

この式について「時間から現在値」と「任意の値までにかかる時間」を算出するということですね。見た目から入るのでとりあえずグラフでイメージを書きます。x0 は x の初期値で、hi 目標値までの距離 ( d – xi ) を表しています。

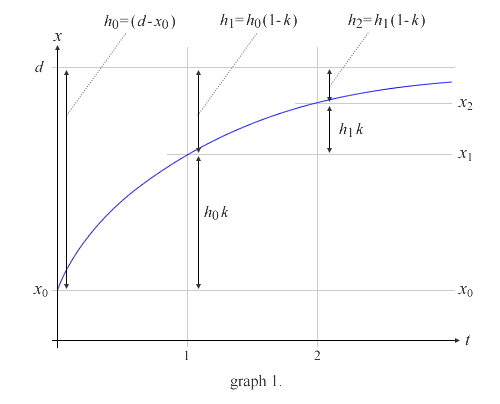
グラフを見ると現在値である x より、目標値までの距離 h が単純な推移をしているような感じです。試しに式にしてみます。 

[xの式] x2 = x1 + (d-x1)*k = x0 + (d-x0)*k + (d-x0)*(1-k)*k
[hの式] h2 = h1*(1-k) = (d-x0)*(1-k)*(1-k) = (d-x0)*(1-k)^2

どうでしょう？
目標値までの距離（残距離）のほうがシンプルに思えませんか？

というわけで、最初の(式1)を残距離の式に直してみると、 

d - x' = d - (x + ( d - x ) * k )
d - x' = ( d - x )*( 1 - k )

これを時間(フレーム)の関数に一般化するには数学的な証明的な必要な雰囲気がありますが、ここはノリでやります。 

残距離(t) = ( d - x0 )*( 1 - k )^t

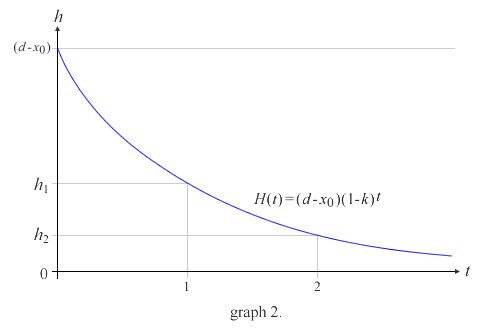
x の値は、移動距離(d-x0)から残距離を引いた値を x0 に加算すればよいので、 

fx(t) = x0 + ( d - x0 ) - ( d - x0 )*( 1 - k )^t

となります。ASの関数にすると、 

/**
* 時間から現在値
* @param   b  初期値
* @param   d  ターゲット
* @param   k  比率(0<k<1)
* @param   n  時間
* @return  時間tでの値
*/
function f2( b:Number, d:Number, k:Number, n:Number ):Number {
  return d - ( d - b )*Math.pow( 1 - k, n );
}

この関数はyossyさんが導いた関数とほぼ同じです。

次に任意の値 D について「Dまでにかかる時間」を求めます。この辺りは Maxima を使って 

f(t):= d - (d-b)*(1-k)^t;
solve( f(t)=D,t );

とすれば、スパっと出てくるんですが、数学的に求めると、「A^x = B」であれば「x=logB/logA」から 

d - ( d - x0 )*( 1 - k )^t = D
  ↓
( 1 - k )^t = ( d - D )/( d - x0)
  ↓
t = log( ( d - D )/( d - x0) )/log( 1 - k)

なので、ASな関数は、 

/**
* 任意の値から時間
* @param   b  初期値
* @param   d  ターゲット
* @param   k  比率(0<k<1)
* @param   D  (b<D<d)
* @return  Dに到達する時間
*/
function f3b( b:Number, d:Number, k:Number, D:Number ):Number {
  return Math.log((d-D)/(d-b)) / Math.log(1-k);
}

これもyossyさんが導いた関数とほぼ同じ。結果同じってことで…。

最後におまけで「時間 t で目標値に到達する k 値」を求めます。これは時間tで残距離が0(に近い)値になるような k を求めればよいので、 

/**
* 任意の値から時間
* @param   b  初期値
* @param   d  ターゲット
* @param   n  到達する時間
* @param   er 閾値(er>0)
* @return  k値
*/
function f4( b:Number, d:Number, n:Number, er:Number=0.001 ):Number {
  return 1 - Math.pow( er/(d-b), 1/n );
}

といった具合になります。

以上、ノリでやってるので間違っていたらすいません。
ともあれyossyさんBetweenAS3はいよいよ完成間近！？なようなので心待ちです。

| INDEX |