12月第1週でゲーム3本購入。なんとも年末気分になっています。前回の流れで3次ベジェ曲線の切り出しを書いてみます。

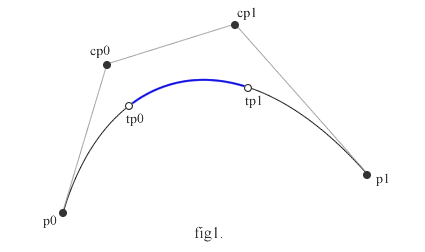
前回のエントリーのように、3次ベジェをtの関数としたとき、t=t0、t=t1での座標は、fig1のようにtp0、tp1となるとします。この間の曲線を切り出すわけですが、次のfig2のような手順でいけます。

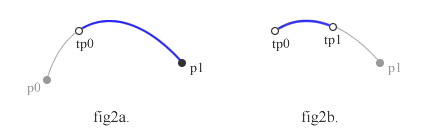
つまり、一度tp0で切り分けて、切り分けられた曲線の一方をtp1で切り分けるんですね。手順としては前回の切り分けを2度行うわけです。

ただ、2度目の切り分け(fig2b)のとき、tp1を示すt値がt1ではなくなります。基準となる曲線が変わるので、t値も変化するわけです。で、t=t1に対応するような、t1’を導きます。

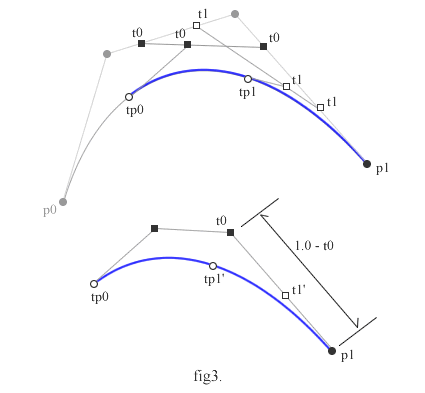
t値を相対的にみると、t1は、長さ 1-t0 の内の t1′ となり、1-t0 を 1 とすると、t1’=(t1-t0)/(1.0-t0) となります。
これを素直にスクリプトにすると、

/**
* Clip Bezier at t0 and t1.
* @param	t0( 0 to 1 )
* @param	t1( 0 to 1 )
*/
/*
_point0:Point 始点
_point1:Point 終点
_control0:Point 制御点
_control1:Point 制御点
*/
function clip( t0:Number, t1:Number ):Object
{
  if( t0==t1 ){
    //同じ値の場合なし
    return null;
  }else if( t0==0 || t0==1 ){
    //端点の場合は切り分けに同じ
    return (split(t1))[ (t0==1)?1:0 ]; //splitって前エントリーで書いた関数
  }else if( t1==0 || t1==1 ){
    //端点の場合は切り分けに同じ
    return (split(t0))[ (t1==1)?1:0 ];
  }

  var p0:Point   = f(t0); //3次ベジェの関数
  var p1:Point   = f(t1);

  //t0で切り分け
  var m0:Point  = Point.interpolate( _control1, _control0, t0);
  var c01:Point = Point.interpolate( _point1, _control1, t0);
  var c00:Point = Point.interpolate( c01, m0, t0);

  //t1'で切り分け
  var t2:Number = (t1-t0)/(1.0-t0);
  var m1:Point   = Point.interpolate( c01, c00, t2);
  var c0:Point = Point.interpolate( c00, p0, t2);
  var c1:Point = Point.interpolate( m1, c0, t2);

  return {p0:p0,p1:p1,cp0:c0,cp1:c1};
}

のような感じです。