久しぶりのエントリーです。仕事が忙しくなると物欲がたくましくなる今日この頃です。年末はゲームもプラモもいろいろ発売でゆるゆるです。バーチャとシュトルヒが欲しい…。で、懲りずにベジェです。3次ベジェの切り分けです。

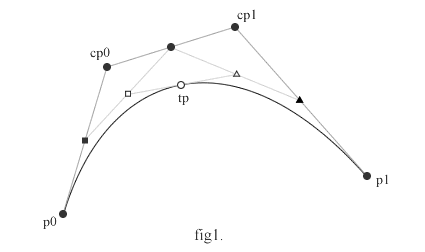
上の図は、3次ベジェを調べたことのある方なら見慣れた図かと思います。図のtpの座標をスクリプトで書くと、

/**
* Bezier Function
* @param	t
* @return	Point
*/
/*
_point0:Point 始点
_point1:Point 終点
_control0:Point 制御点
_control1:Point 制御点
*/
function f(t:Number):Point
{
  var tp:Number = 1.0 - t;
  return new Point( _point0.x*tp*tp*tp + 3*_control0.x*t*tp*tp + 3*_control1.x*t*t*tp + _point1.x*t*t*t,
                    _point0.y*tp*tp*tp + 3*_control0.y*t*tp*tp + 3*_control1.y*t*t*tp + _point1.y*t*t*t );
}

な感じのtに関する関数になります。
で、任意のt値、例えばポイントtpで3次ベジェを2つに分けようというものです。

2つに分けるには、2つの3次ベジェの新しい制御点を求めることになりますが、図を眺めているとすでに見えているのですね。2分割した後の曲線は、以下の図のようになります。勢いでやってみると、案外すんなりいくものです。

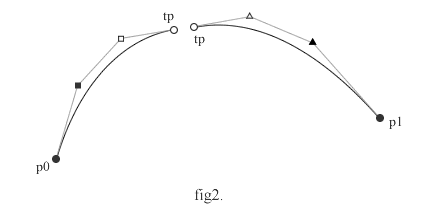
図でいうところの、■□、△▲が新しい制御点になります。
ベタにスクリプトで書くと、

/**
* Split Bezier at t.
* @param	t( 0 to 1 )
*/
function split(t:Number):Array
{
  var tp:Point   = f(t); //上に書いた関数
  var m:Point   = Point.interpolate( _control1, _control0, t);

  //制御点■□
  var ac0:Point = Point.interpolate( _control0, _point0, t);
  var ac1:Point = Point.interpolate( m, ac0, t);

  //制御点△▲
  var bc1:Point = Point.interpolate( _point1, _control1, t);
  var bc0:Point = Point.interpolate( bc1, m, t);

  return [ {p0:_point0.clone(),p1:tp,cp0:ac0,cp1:ac1},
           {p0:tp.clone(),p1:_point1.clone(),cp0:bc0,cp1:bc1}];
}

のような感じです。

青、オレンジの曲線が切り取った線で、中の黒い線がもともとの曲線です。

SVGの読み込みをしようと思って、その過程で3次ベジェを2次ベジェに変換したくて、その前処理に使ったりしてます。