| INDEX |

[as]ベジェ曲線の分割(2) 破線の描画

9月 28, 2007

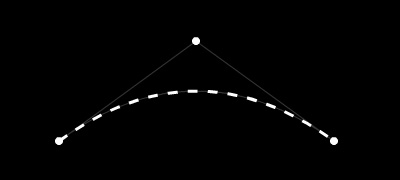
ベジェ曲線の分割の流れで、ActionScriptでベジェ曲線を破線で描画してみます。

前回、等分の座標を求めるのに、変数tを0から1まで小刻みに増やして逐一チェックする方法をとっていました。この部分を若干汎用化して、任意の長さからt値を得るようにしてみました。 

/**
* 長さからtを得る
* @param  長さ( 0～length：曲線の長さ )
* @param  許容誤差
* @return t
*/
public function length2T( len:Number, d:Number=0.1 ):Number{
  if( len<0 || len>_length ){
    //0以下、曲線より大きい場合NaN
    return Number.NaN;
  }else{
    //再帰的関数でt値を得る
    return seekL( len, d );
  }
}

/**
* 長さに対するtを得る
* @param  長さ( 0～length )
* @param  許容誤差
* @param  チェックt値
* @param  次のチェックt値差分
* @return t
*/
private function seekL( len:Number, d:Number=0.1, t0:Number=0.5, td:Number=0.25  ):Number{
  //積分して長さを得る
  var lent0:Number = integral(t0);
  if( Math.abs( len-lent0 )<d ){
    //許容誤差以内なら確定
    return t0;
  }else{
    //再帰的に次のチェックへ
    return seekL( len, d, (lent0<len) ? t0+td : t0-td, td/2 );
  }
}

こんな感じになります。と言っても見た目変わりませんが…。

任意の長さでt値を得るので、順繰りにt値を調べるより、分割数が少ないのであれば処理負荷が減ります。順繰りで調べるときのt値差分を0.001、長さから調べる場合の長さ誤差を0.1とすると、分割数50ぐらいが同程度の負荷か、といった具合です。
また、長さから調べる方が汎化的なので、スクリプトがシンプルになります。 

//分割数
var sn:Number = 20;

//率差分
var kd:Number = 1.0/sn;

plots.graphics.clear();
for( var k:Number=kd; k


上のサンプルでは、分割点に円をプロットしていますが、点をもっと細かくすれば点線になります。

で、これを破線にしたいなぁ、という感じです。




破線で描く場合、分割座標をもとに曲線を分割するわけですが、実際描画するには分割曲線のコントロール点が必要になります。コントロール点がないと、破線が直線になってしまうのですね。

今回、コントロール点を求めるのに、分割曲線両端の微分(ベクトル)を使ってみます。




分割曲線の両端を、p0,p1として、p0からp1のベクトルをpvとします。pvは両端を結ぶ直線ですね。で、両端それぞれの位置で微分して得たベクトルを、pv0、pv1とします。微分で得たベクトルは曲線に対して接線になっています。ですので、コントロール点は、pv0、pv1の上、或いは延長上の交点にあれば、元の曲線に対して滑らかな曲線になるわけです。

ベクトル的な見方をすると、pv = a*( pv0 + pv1 ) になればいい感じです。



//破線長
var ds:Number = 10;

//分割数
var sn:Number = bezje.length/ds;

//率
var kd:Number = 1.0/sn;

graphics.lineStyle(3,0xffffff,1.0,false,"normal","none");
for( var k:Number=0; k<1.0 ; k+=kd*2 ){
  //線分始点位置
  var len0:Number = bezje.length*k;
  //線分終点位置
  var len1:Number = bezje.length*Math.min( k+kd, 1.0 );
  
  //差が閾値以下は描画なし
  if( len1-len0>=1.0 ){
    var t0:Number = bezje.length2T( len0, 0.1 );
    var t1:Number = bezje.length2T( len1, 0.1 );
    
    //両端の座標とベクトル
    var pv0:Point = bezje.diff(t0);
    var pp0:Point = bezje.f(t0);
    var pv1:Point = bezje.diff(t1);
    var pp1:Point = bezje.f(t1);
    
    //両端の差分
    var dx:Number = pp1.x-pp0.x;
    var dy:Number = pp1.y-pp0.y;
    
    // Point(dx,dy) = a*(pv0 + pv1) のaを求める
    var a:Number;
    if( dx != 0 ){
      a = dx/(pv1.x+pv0.x);
    }else{
      a = dy/(pv1.y+pv0.y);
    }
    
    //線分描画
    graphics.moveTo( pp0.x, pp0.y );
    graphics.curveTo( pp0.x + a*pv0.x, pp0.y + a*pv0.y, pp1.x, pp1.y );
  }
}




こんな感じになります。






※ベジェ曲線の積分で、3点が直線上に並ぶとバグるところは修正しました。




>> source

| INDEX |