ActionScriptのGraphics.curveToで描画する2次のベジェ曲線を等分する座標を求めてみます。とりあえずベタな方法です。
2次のベジェ曲線は、curveToで描画するものですが、関数で表現すると次のようになります。
_point0は始点、_point1は終点、_controlはコントロール点です。
/**
* ベジェ関数
* @param t( 0~1.0 )
* @return 座標
*/
function f(t:Number):Point{
var tp:Number = 1.0 - t;
return new Point( _point0.x*tp*tp + 2*_control.x*t*tp + _point1.x*t*t,
_point0.y*tp*tp + 2*_control.y*t*tp + _point1.y*t*t );
}
この関数は、3次ベジェと同様に変数t(0~1)の関数で、この関数を使えば、curveToで描画した線上に沿って、DisplayObjectなどを動かしたりできます。
>> こんな感じ
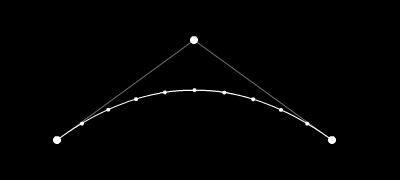
で、tを等分に、例えば0.1刻みで座標を求めると、次のような感じです。等分にはならないわけですね。
※一応ポイントをドラッグできます。
これを等分にしたいわけですが、とりあえずベタな方法を使って、長さが等分なt値を求めてみます。ベタな方法というのは、tを小刻みに増やして、目的の長さまで調べる、といった方法です。ベタです。
任意のtについて曲線の長さを求めるには、2次ベジェ関数の積分を行う必要がありますが、積分方法はこんな感じです。
※しっかりつくってないので、曲線が直線になったりするとバグります。
//等分な長さのtを得る
//分割数
var sn:Number = 10;
//分割差分
var dlen:Number = bezje.length/sn;
//tの精度
var dt:Number = 0.001;
var tmp_len:Number = dlen;
var tmp_n:int = 1;
for( var t:Number=0; t<=1.0 ; t+=dt ){
var len:Number = bezje.integral(t); //ここは積分
if( len>=tmp_len ){
tmp_n++;
if( tmp_n==sn ){
break;
}
tmp_len = dlen*tmp_n;
}
}
この方法ですと、当り前ですが小刻みの具合(上記dt)によって精度が随分かわります。もちろん処理負荷も。ループの回し方にいろいろ工夫ができそうですが、とりあえずここまでで。