2つの円に共通する接線を求めてみようと思います。接線は、それぞれの円の接点を求めることと同じになりますが、この接点は、Math.acos でわりと単純に求めることができます。

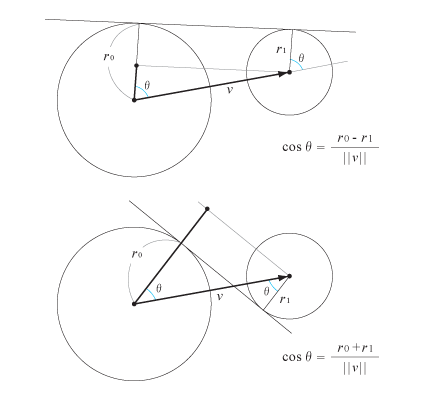
上の図のように、2つの円の中心を結ぶベクトルをvとします。接線ができるのは、2つの円について、vからの角度が同じθの場合と、θとθ+Math.PI の場合です。どちらも、vの角度から±θのところが接点になります。また、θとθ+Math.PIの場合は、2つの接線が交差します。

cosθは、上図のような関係になるので、θは、

a1 = Math.acos( (r0-r1)/v.length );
a2 = Math.acos( (r0+r1)/v.length );

で求めることができます。θは、(r0-r1)、(r0+r1)が、v.lengthより大きい場合は成立しませんから、その場合、接線はないことになります。

接点の座標は、vの角度から±θになるので、

/**
* 円0: 中心( x0, y0 ) 半径 r0
* 円1: 中心( x1, y1 ) 半径 r1
*
*/
dr:Number = r0-r1;
if( Math.abs(dr)<=v.length ){
  //接線あり
  
  //vの角度
  var a0:Number = Math.atan2( v.y, v.x );
  
  //接点の角度１
  var a1:Number = Math.acos( dr/v.length );
  
  //円0の接点
  var tp01:Point = new Point( x0 + r0*Math.cos(a0+a1), y0 + r0*Math.sin(a0+a1) );
  var tp02:Point = new Point( x0 + r0*Math.cos(a0-a1), y0 + r0*Math.sin(a0-a1) );
  
  //円1の接点
  var tp11:Point = new Point( x1 + r1*Math.cos(a0+a1), y1 + r1*Math.sin(a0+a1) );
  var tp12:Point = new Point( x1 + r1*Math.cos(a0-a1), y1 + r1*Math.sin(a0-a1) );
  
  dr = r0+r1;
  if( dr<v.length ){
    //接点の角度２
    var a2:Number = Math.acos( dr/v.length );
    
    //円0の接点
    var tp03:Point = new Point( x0 + r0*Math.cos(a0+a2), y0 + r0*Math.sin(a0+a2) );
    var tp04:Point = new Point( x0 + r0*Math.cos(a0-a2), y0 + r0*Math.sin(a0-a2) );
    
    //円1の接点
    var tp13:Point = new Point( x1 + r1*Math.cos(a0+a2+Math.PI), y1 + r1*Math.sin(a0+a2+Math.PI) );
    var tp14:Point = new Point( x1 + r1*Math.cos(a0-a2+Math.PI), y1 + r1*Math.sin(a0-a2+Math.PI) );
    
  }else if( dr==v.length ){
    //円が接している 接点
    var tp05:Point = new Point( x0 + r0*Math.cos(a0), y0 + r0*Math.sin(a0) );
  }
}

のようになります。

接線だけなら、a0、a1、a2を求めて、円1についての接線を求めればよいことになります。

>> source